Average speed and average velocity are not the same quantity, and they are calculated differently. This is not just because velocity is a vector and speed is not; it has to do with distance and displacement. On this page we'll show you how to calculate both average speed and average velocity, and explain why they're different.
Average speed is not a vector quantity. It has no direction.
The simplest way to find average speed is to divide the total distance travelled by the total time taken.
Have a look at the path followed by the child shown below.
She has travelled a total distance of 12 metres, and has stopped 3 metres from where she began.
Average speed is not a vector quantity. It has no direction.
The simplest way to find average speed is to divide the total distance travelled by the total time taken.
Have a look at the path followed by the child shown below.
She has travelled a total distance of 12 metres, and has stopped 3 metres from where she began.
Let's suppose she covered each leg of her journey in one second. This means that the total time for her trip was
Her average speed is the total distance she covered, divided by the total time taken.
Since she covered a total distance of 12 metres in 6 seconds , her average speed for the trip is 2 m/s.
Which direction she went, or where she ended up, is unimportant, as long as we know the sum of all the distances she travelled, and how long it took.
Which direction she went, or where she ended up, is unimportant, as long as we know the sum of all the distances she travelled, and how long it took.
A Few More Examples:
Example:
A car travels between 2 towns 60 miles apart in 2 hours. What is its average speed?
Answer:
average speed = distance/time Therefore, the average speed of the car is 60 miles/2 hours = 30 miles/hour.
Example:
If a person can walk with an average speed of 2 meters/second, how far will they walk in 4 minutes?
Answer:
There are 60 seconds in 1 minute, so there are 4 (60 seconds) = 240 seconds in 4 minutes. Also, if average speed = distance/time, then distance = (average speed)(time). Therefore, the distance the person moves is (2 m/s)(240 s) = 480 meters.
Speed Units
Since average speed is always calculated as a distance (length) divided by a time, the units of average speed are always a distance unit divided by a time unit. Common units of speed are meters/second (abbreviated m/s), centimeters/second (cm/s), kilometers/hour (km/hr), miles/hour (mi/hr - try to avoid the common abbreviation mph), and many others.
Example:
Which of the following could be a speed measurement?
- 2.5 meters
- 2.5 seconds/meter
- 2.5 meters/second
- 2.5 meters/second/second
Answer:
Only 2.5 meters/second could be a speed measurement. Speed always has units of a distance (length) unit divided by a time unit.
Which Distance?
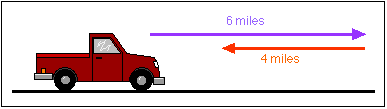 |
| Farmer Jones drives 6 miles down a straight road. She turns around and drives 4 miles back. What was her average speed for this trip if it took 1 hour? |
Your answer to this problem depends on your interpretation of "distance traveled". You could say:
- The total distance traveled by Farmer Jones is 10 miles. Therefore her average speed is 10 mi/hr.
- The net distance traveled by Farmer Jones is 2 miles. Therefore, her average speed is 2 mi/hr.
There are good reasons to use either interpretation - it's mostly a matter of preference. We will interpret "distance traveled" to be net distance (also calleddisplacement). Farmer Jones' average speed was 2 mi/hr.
NOTE: Different texts may adopt other conventions! In fact, our AP Physics text uses total distance to calculate speed, but net distance to calculate velocity. Use caution here!
The Perils of Averaging Averages
Here is an interesting problem:
Susie has planned a trip to a city 60 miles away. She wishes to have an average speed of 60 miles/hour for the trip. Due to a traffic jam, however, she only has an average speed of 30 miles/hour for the first 30 miles. How fast does she need to go for the remaining 30 miles so that her average speed is 60 miles/hour for the whole trip?
Most likely you thought "Oh, 90 miles/hour - since the average of 30 and 90 is 60! Boy, this is easy!"
Unfortunately, however, the answer is not 90 miles/hour. Here's why: You know that average velocity = distance/time (v = d/t). In order to have an average speed of 60 miles/hour over a distance of 60 miles, you must complete the trip in 1 hour:
60 miles/hour = distance/ time = 60 miles/ 1 hour
Notice that it would take 1/3 of an hour to cover the last 30 miles at 90 miles/hour. The total time for her trip would be 1.33 hours, and her average speed would be:
v = distance/ time = 60 miles/ 1.33 hours = 45 miles/ hour
Try this calculation for any speed for the second half of the trip - the average speed for the whole trip cannot ever be 60 miles/hour! The moral of the story: Don't average averages!
Measuring Speed Activity
This would be a good time to do the Measuring Speed Activity, in which you:
- determine some average speeds by measuring distances and times, and
- determine an unknown distance by measuring time to cover the distance at a known speed

